Relating Tuning and Timbre
![]()
This is the full text of the article (more or less) as it first appeared in Experimental Musical Instruments. It was the catalyst for much of the work that resulted in Tuning Timbre Spectrum Scale, and it contains links to computer programs that will make it easy for you to draw dissonance curves yourself. James Forrest has recently created a Java applet for interactive exploration of dissonance curves.
"Clearly the timbre of an instrument strongly affects what tuning and scale sound best on that instrument" W. Carlos
If you've ever attempted to play music in weird tunings (where "weird" means anything other than 12 tone equal temperament), then you've probably noticed that certain timbres (or tones) sound good in some scales and not in others. 17 and 19 tone equal temperament are easy to play in, for instance, because many of the standard timbres in synthesizers sound fine in these tunings. I remember when I first played in 16 tone. I had to audition hundreds of sounds before I found a few good timbres. When I tried to play in 10 tone, though, none of the timbres in my synthesizers sounded good. This article explains why this happens, and shows how to design timbres and scales that complement each other. This suggests a way to design new musical instruments with unusual timbres that can play consonantly in unusual scales.
The principle of local consonance describes a relationship between the timbre of a sound and a tuning (or scale) in which the timbre will sound most consonant. The principle answers two complementary questions. Given a timbre, what scale should it be played in? Given a scale, how can consonant timbres be chosen? The ability to answer such questions will likely impact the way we design new musical instruments.
The presentation begins in the next section with an overview of the work of several acousticians, who have shown that people consistently judge the consonance of intervals composed of pure sine waves. These judgements are averaged into a "consonance curve" which is used to calculate the consonance of complex timbres. The results of such calculations agree well with the normal (musical) notion of consonance when applied to harmonic timbres. Thus unisons, octaves, fifths and fourths are highly consonant while seconds and sevenths are relatively dissonant.
Of course, this measure of consonance can also be applied to other (non-harmonic) timbres, and the succeeding sections show how to design timbres and scales. Several concrete examples follow, including finding scales for nonharmonic timbres (the natural resonances of a uniform beam, "stretched" and "compressed" timbres, FM timbres with noninteger carrier to modulation ratios), and finding timbres for equal tempered scales. This article is a less technical presentation of my paper "Local Consonance and the Relationship Between Timbre and Scale," which contains the mathematical details.
The standard musicological definition (see your favorite dictionary) is that a musical interval is consonant if it sounds pleasant or restful; a consonant interval has little or no musical tension or tendency to change. Dissonance, on the other hand, is the degree to which an interval sounds unpleasant or rough; dissonant intervals generally feel tense and unresolved.
In On the Sensations of Tones, Helmholtz offers a physiological explanation for consonance that is based on the phenomenon of beats. If two tones are sounded at almost the same frequency, then a distinct beating occurs that is due to interference between the two tones (piano tuners use this effect regularly). The beating becomes slower as the two tones move closer together, and completely disappears when the frequencies are identical. Typically, slow beats are percieved as a pleasant vibrato while fast beats tend to be rough and annoying. Recalling that any timbre can be decomposed into sine wave components, Helmholtz theorized that dissonance between two tones is caused by the rapid beating of various sine wave components. Consonance, according to Helmholtz, is the absence of such dissonant beats.
More recently, Plomp and Levelt (full references are at the end) examined consonance experimentally, by generating pairs of sine waves and asking volunteers to rate them in terms of their relative consonance. Despite considerable variability among the responses, there was a simple and clear trend. At unison, the consonance was maximum. As the interval increased, it was judged less and less consonant until at some point a minimum was reached. After this, the consonance increased up towards, but never quite reached the consonance of the unison. Plomp and Levelt called this tonal consonance, to distinguish it from musical consonance and from Helmholtz' beat theory.
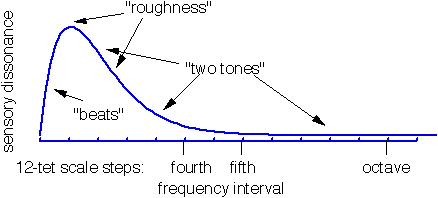
The above figure shows an averaged version of the dissonance curve (which is simply the consonance curve flipped upside-down) in which dissonance begins at zero (at an "interval" of a unison) increases rapidly to a maximum, and then falls back towards zero. The most surprising feature of this curve is that the musically consonant intervals are undistinguished - there is no dip in the curve at the fourth, fifth, or even the octave.
Figure 2: A harmonic timbre with six partials is used to generate the dissonance curve of figure 3. Amplitudes fall at a rate of 0.88. The frequency axis is normalized so that the root frequency is unity.
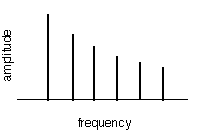
To explain perceptions of musical intervals, Plomp and Levelt note that most traditional musical tones have a spectrum consisting of a root or fundamental frequency, and a series of sine wave partials that occur at integer multiples of the fundamental. Figure 2 depicts one such timbre. If this timbre is sounded at various intervals, the dissonance of the intervals can be calculated by adding up all of the dissonances between all pairs of partials. Carrying out this calculation for a range of intervals leads to the dissonance curve. For example, the dissonance curve formed by the timbre of figure 2 is shown below in figure 3.
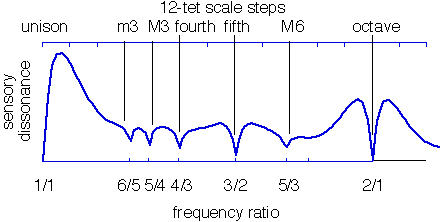
Observe that this curve contains major dips at many of the intervals of the 12 tone equal tempered scale. The most consonant interval is the unison, followed closely by the octave. Next is the fifth, followed by the fourth, the major third, the major sixth, and the minor third. These agree with standard musical usage and experience. Looking at the data more closely shows that the minima do not occur at exactly the scale steps of the 12 tone equal tempered scale. Rather, they occur at the "nearby" simple ratios 1:1, 2:1, 3:2, 4:3, 5:4, and 5:3 respectively, which are exactly the locations of notes in the "justly intoned" scales (see Wilkinson). Thus an argument based on tonal consonance is consistent with the use of just intonation (scales based on intervals with simple integer ratios), at least for harmonic timbres.
Perhaps the most striking aspect of figure 3 is that most of the scale steps of the major scale are roughly coincident with local minima of the dissonance curve. Thus the ear perceives intervals which occur at points of local minima in the dissonance curve as relatively consonant. This observation forms the basis of the principle of local consonance:
A timbre and a scale are said to be related if the timbre generates a dissonance curve whose local minima occur at scale positions.
This notion of relatedness of scales and timbres suggests two interesting avenues of investigation. Given an arbitrary timbre T (perhaps one whose spectrum does not consist of a standard harmonic series), it is straightforward to draw the dissonance curve generated by T. The local minima of this curve occur at values which are good candidates for notes of a scale, since they are local points of minimum dissonance (i.e. maximum consonance). This might be useful to the experimental musician. Imagine being in the process of creating a new instrument with an unusual (i.e., non-harmonic) tonal quality. How should the instrument be tuned? To what scale should the finger holes (or frets, or whatever) be tuned? The principle of local consonance answers this question in a concrete way.
Alternatively, given a desired scale (perhaps one which divides the octave into n equal pieces, or one which is not based on the octave), there are timbres which will generate a dissonance curve with local minima at precisely the scale degrees. This is useful to musicians and composers who wish to play in nonstandard scales such as 10 tone equal temperament.
As the opening quote indicates, this is not the first time that the relationship between timbre and scale has been explored. Pierce's brief note reported synthesizing a timbre designed specifically to be played in an 8 tone equal tempered scale. Pierce concludes, "... by providing music with tones having accurately specified but nonharmonic partials, the digital computer can release music from the tyranny of 12 tones without throwing consonance overboard." Slaymaker investigated timbres with stretched (and compressed) partials, and Mathews and Pierce explored their potential musical uses. Recently, Mathews and Pierce examined a scale with steps based on the thirteenth root of three, rather than the standard twelfth root of two, which is designed to be played with timbres containing only odd partials. Carlos investigated scales for nonharmonic timbres by overlaying their spectra and searching for intervals in which partials coincide, thus minimizing the beats (or roughness) of the sound. This is similar to the present approach, but we provide a systematic technique that can be used to find scales for a given timbre, or to find timbres for a given scale.
It would be naive to suggest that truly musical properties can be measured as a simple tonal consonance. Even in the realm of harmony (and ignoring musically essential aspects such as melody and rhythmn), consonance is not the whole story. Indeed, a harmonic progression that was uniformly consonant would likely be boring. Harmonic interest arises from a complex interplay of dissonance (restlessness) and consonance (rest). Perhaps the most important use of the principle of local consonance is to provide guidelines for exploring new tonalities and tunings.
If you're thinking that there must be a lot of calculations necessary to draw dissonance curves, you're right. It's an ideal job for a computer.
Those familiar with MATLAB, BASIC or related computer languages may wish to look at the program. The program works by encapsulating the Plomp-Levelt consonance curve into a mathematical function that consists of a sum of exponentials. The i and j loops calculate the dissonance of the timbre at a particular interval alpha, and the alpha loop runs through all the intervals of interest. The first few lines set up the frequencies and amplitudes of the timbre. The variable n must be equal to the number of frequencies in the timbre. Running the program as is generates the dissonance data of figure 3 for the timbre of figure 2. To change the start and end points of the intervals, use startint and endint. To make the intervals further apart, increase inc. All the dissonance values are stored in the vector diss. Don't change dstar or any of the variables with numbers.
Fortunately, there are some general patterns in the ways that dissonance curves can look. Let's examine a simple timbre with just two partials. As shown in figure 4, the dissonance curve can have three different contours: if the partials are very close together then there are no points of local consonance, if the partials are widely separated then there are two local minima, if they are in between then there is just one. Using the program, you can reproduce these curves (or, of course, generate your own). Set n=2 and freq(1)=500, freq(2)=505, amp(1)=10, amp(2)=10. This gives figure 4(a), where the partials are too close to allow a point of local consonance. Setting freq(2)=1.15*500 shows that the point of local consonance occurs at an interval of 1.15, as in 4(b). Finally, setting freq(2)=1.86*500 gives 4(c), with two points of local consonance. The steep minimum occurs at an interval of 1.86. Notice that the second minimum is shallow, and is a result of the large distance between the partials of the timbre.
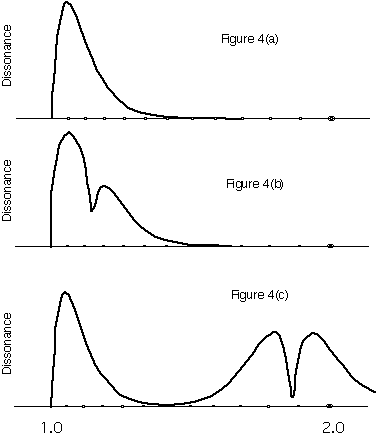
You can listen to figure 4 with a synthesizer or tone generator. First, find a tone that is as close to a sine wave as possible. (If using a sample based machine without such a humble waveform, try an organ or flute sample). Assign two tones to each keypress, one at frequency f, and one at a major seventh above f. (A major 7th is an interval of 1.86, just as in 4(c)). Listen to the consonance of the various intervals in this timbre. The first few are very rough. The next few are somewhat aharmonic, but not unpleasant. Then the dissonance rises and plummets quickly, at the interval of 1.86. The octave, at an interval of 2, sounds very dissonant and unoctavelike. For this timbre, the major 7th plays the role normally occupied by the octave, at least in terms of consonance. This is something you can hear for yourself.
Here are some general properties of dissonance curves. Suppose that the timbre F has n partials located at frequencies (f1, f2, ... , fn).
Property 1: The unison is the global minimum (the lowest possible value of the dissonance curve). All other minima are local.
Property 2: As the interval grows larger, the dissonance must approach a value that is no more than the intrinsic dissonance of the timbre.
Property 3: The dissonance curve generated by F has at most 2n(n-1) local minima which are located symmetrically (on a logarithmic scale) so that half occur for intervals between 0 and 1, and half occur for intervals between 1 and infinity.
Property 4: Up to half of the local minima occur at intervals a for which a=fi /fj where fi and fj are arbitrary partials of F. Up to half of the local minima are the shallow type of figure 4(c).
The fourth property is particularly interesting because it says that points of local consonance tend to occur at intervals which are simply defined by the partials of the timbre. In figures 4(b) and 4(c), for instance, local minima are found at a=1.15 and a=1.86 respectively, which is the ratio between the two partials. The musically useful information is usually contained in intervals between 1/m and m for some small m. The shallow minima tend to vanish for timbres with more than a few partials. Figure 3, for instance, consists exclusively of local minima caused by coinciding partials. Thus, dissonance curves usually have fewer than 2n(n-1) local minima. In figure 3, for instance, there are only 7 local minima within the octave of interest, considerably fewer than the theoretical maximum of 84. It is possible to achieve the bound. For instance, the timbre (f,2f,3f) over the range 0<a<6 exhibits all 12 possible minima.
This section constructs examples of scales appropriate for a variety of timbres, and explains various consonance related phenomena in terms of the principle of local consonance.
The points of local consonance for the harmonic timbre with partials at (f, 2f, ... , 7f ) are located at simple integer ratios. The results of the previous section explain this elegantly. Candidate points of local consonance are at intervals a for which fi = a fj. Since the partials are at integer multiples of f, a=n/m for integers n and m between 1 and 7. The principle of local consonance says that the most appropriate scale tones for harmonic timbres are located at such a, and indeed, all the points of local consonance of figure 3 occur at such values. The following table compares intervals in the 12-tet scale, intervals in the just major scale, and minima of a dissonance curve drawn for a timbre with nine harmonic partials.
|
|
|
|
|
| C | 1.0 |
1.0 |
1:1 |
unison |
| C# | 1.059 |
16:15 |
just semitone | |
| D | 1.122 |
1.14 (8:7 = sept. maj. 2) |
9:8 |
just whole tone |
| D# | 1.189 |
1.17 (7:6 = sept. min 3) |
||
|
1.2 (6:5) |
6:5 |
just min. 3 | ||
| E | 1.26 |
1.25 (5:4) |
5:4 |
just maj. 3 |
| F | 1.335 |
1.33 (4:3) |
4:3 |
just perfect 4 |
| F# | 1.414 |
1.4 (7:5 = sept. tritone) |
45:32 |
just tritone |
| G | 1.498 |
1.5 (3:2) |
3:2 |
perfect 5 |
| G# | 1.587 |
1.6 (8:5) |
8:5 |
just min. 6 |
| A | 1.682 |
1.67 (5:3) |
5:3 |
just maj. 6 |
| A# | 1.782 |
1.75 (7:4 = sept. min. 7) |
16:9 |
just min. 7 |
| B | 1.888 |
1.8 (9:5 = large just maj. 7) |
15:8 |
just maj. 7 |
| C | 2.0 |
2.0 |
2:1 |
octave |
In a sense, this provides a psychoacoustic basis for justly intonated scales. In terms of tonal consonance, the ear is fairly insensitive to small deviations in frequency, and the 12 tone equal tuning can be viewed as an acceptable compromise between the consonance based desire to play in justly intoned scales and the practicalities of instrument standardization.
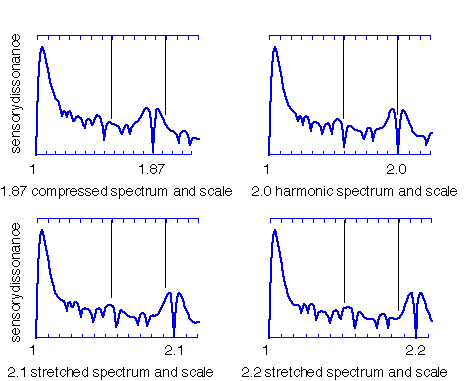
Slaymaker and Mathews and Pierce have investigated timbres with partials at fj = f Alog( j) where the log is taken base 2. When A=2, this is simply a harmonic timbre, since fj = f 2log(j)= jf. When A<2, the frequencies of the timbre are compressed, while when A>2, the partials are stretched. The most striking aspect of compressed and stretched timbres is the lack of a real octave. This can be seen clearly from the dissonance curves, which are plotted in the four panels of the figure for A=1.87, 2.0, 2.1, and 2.2 respectively. In each case, the frequency ratio A plays the role of the octave, which Mathews and Pierce call the pseudo octave. Real octaves sound dissonant and unresolved when A is different from 2 while the pseudo octaves are highly consonant. More importantly, each curve has a similar contour. Points of local consonance occur at (or near) the twelve equal steps of the pseudo octaves. "Pseudo-fifths," "pseudo-fourths," and "pseudo-thirds" are readily discernable. This suggests that much of music theory and practice can be transferred to to compressed and stretched timbres, when played in compressed and stretched scale
It is well known that xylophones, and other instruments which consist of beams with free ends, have partials which are not harmonically related. The principle of local consonance suggests that there is a natural scale, defined by the timbre of the xylophone, in which it will sound most consonant. The first seven frequencies of an ideal beam which is free to vibrate at both ends are given by Fletcher and Rossing as
f, 2.758f, 5.406f, 8.936f, 13.35f, 18.645f, 24.82f .
Two octaves of the dissonance curve for this timbre are shown below. The curve has numerous minima which are spaced unevenly at the frequencies shown.
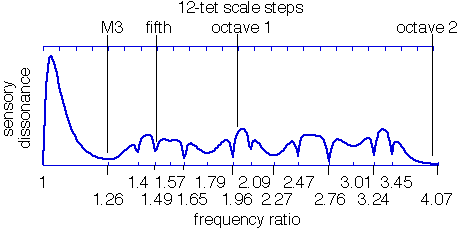
This suggests that these would be the most natural sounding tuning for a xylophone, at least in terms of consonance.
One common method of sound synthesis is frequency modulation (FM) (see Chowning). Noninteger ratios of the carrier and modulating frequencies give nonharmonic timbres that are typically relegated to percussive or bell patches because they sound dissonant when played in traditional 12 tone harmonies. The principle of local consonance suggests that such sounds can be played more harmoniously in scales which are determined by the timbres themselves. A Java applet by James Forrest allows immediate and hands-on exploration of FM timbres and their dissonance curves. The program also maps the sounds onto your computer keyboard so that they are easy to play.
For example, consider a simple FM tone with carrier to modulator ratio c:m of 1:1.4 and modulating index I=2. The frequencies and amplitudes of the resulting timbre are given in the following figure.
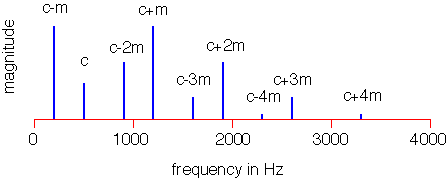
Three octaves of the dissonance curve for this FM timbre are plotted below. The appropriate scale notes for this timbre occur at the minima of the dissonance curve, which can be read directly from the figure.
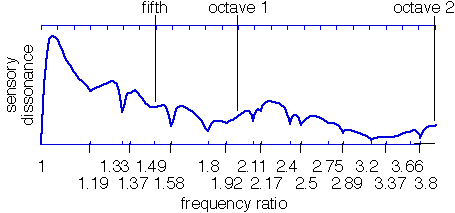
The optimal scale for a given timbre is found simply by locating the local minima of the dissonance curve. The complementary problem of finding an optimal timbre for a given scale is not as simple. There is no single "best" timbre for a given scale. But it is often possible to find "locally best" timbres which can be specified as the solution to a certain optimization problem. For certain classes of scales (such as the m-tone equal tempered scales) the properties of the dissonance curve can be exploited to solve the problem efficiently.
Any set of m scale tones specifies a set of m-1 intervals a1, a2, ... , am-1. The naive approach to the problem of timbre selection is to chose a set of n partials (f1, f2, ... , fn) and volumes (or amplitudes) (v1, v2, ... , vn) to minimize the sum of the dissonances over the m-1 intervals. Unfortunately, this can lead to "trivial" timbres in two ways. Zero dissonance can be achieved by setting all the amplitudes to zero, or by allowing the ai to become arbitrarily large (recall property 2). To avoid such trivial solutions, some constraints are necessary:
Constraint 1: Don't allow the amplitudes to change.
Constraint 2: Force all frequencies to lie in a predetermined region.
The revised (constrained) optimization is then: With the amplitudes fixed, select a set of n frequencies (f1, f2, ... , fn) lying in the range of interest so as to minimize the cost
C = w1 ( sum of dissonances ) + w2 ( number of points )
over the m-1 intervals of local minima, where the w1 and w2 are weighting factors. Minimizing this cost C tends to place the scale steps at local minima as well as to minimize the value of the dissonance curve. Experimentally, we have found that weightings of about w1/w2 = 1000/1 seem to give reasonable results.
Minimizing the cost C is a n-dimensional optimization problem with a highly complex error surface. Fortunately, such problems can be solved adequitely (though not necessarily optimally) using a variety of "random search" methods such as "simulated annealing," (see Kirkpatrick) or the "genetic algorithm" (see Goldberg).
The genetic algorithm (GA) seems to work well. The GA requires that the problem be coded in a finite string called the "gene" and that a "fitness" function be defined. Genes for the timbre selection problem are formed by concatenating binary representations of the fi. The fitness function of the gene (f1, f2, ... , fn) is measured as the value of the cost J above, and timbres are judged "more fit" if the cost C is lower. The GA searches n-dimensional space measuring the fitness of timbres. The most fit are combined (via a "mating" procedure) into "child timbres" for the next generation. As generations pass, the algorithm tends to converge, and the most fit timbre is a good candidate for the minimizer of C. Indeed, the GA tends to return timbres which are well matched to the desired scale in the sense that scale steps tend to occur at points of local consonance and the total dissonance at scale steps is low. For example, when the 12 tone equal tempered scale is specified, the GA converges near harmonic timbres quite often. This is a good indication that the algorithm is functioning and that the free parameters have been chosen sensibly.
As an example of the application of the genetic algorithm to the timbre selection problem, a desired scale was chosen with scale steps at 1, 1.1875, 1.3125, 1.5, 1.8125, and 2. A set of amplitudes were chosen as 10, 8.8, 7.7, 6.8, 5.9, 5.2, 4.6, 4.0, and the GA was allowed to search for the most fit timbre. The frequencies were coded as 8 bit binary numbers with 4 bits for the integer part and 4 bits for the fractional part. The best three timbres out of 10 trial runs of the algorithm were
(f, 1.8f, 4.9f, 14f, 9.87f, 14.81f, 6.4f, 12.9f)
(f, 1.5f, 3.3f, 10.3f, 7.8f, 7.09f, 3.52f, 3.87f)
(f, 2.39f, 9.9275f, 7.56f, 11.4f, 4.99f, 6.37f, 10.6f)
The dissonance curve of the best timbre is shown below. Clearly, these timbres are related to the specified scale, since points of local consonance occur precisely at the scale steps.
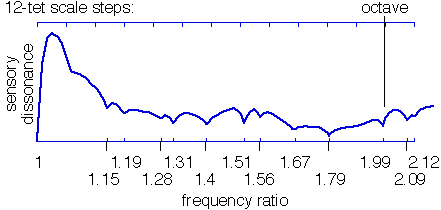
For certain scales, such as the m-tone equal tempered scales, properties of the dissonance curve can be exploited to quickly and easily design timbres, thus bypassing the need to run an optimization program. Recall that the ratio between successive scale steps in 12 tone equal temperament is the twelfth root of 2 (about 1.0595). Similarly, m-tone equal temperament has a ratio of b=mth root of 2 between successive scale steps. Consider timbres for which successive partials are ratios of powers of b. Each partial of such a timbre, when transposed into the same octave as the fundamental, lies on a note of the scale. Such a timbre is said to be induced by the m-tone equal tempered scale. For example, harmonic timbres are induced timbres for the justly intoned scale.
Induced timbres are good candidate solutions to the optimization problem. Recall from property 4 that points of local consonance tend to be located at intervals a for which fi = a fj where fi and fj are partials of the timbre F. Since the ratio between any pair of partials in an induced timbre is bk for some integer k, the dissonance curve will tend to have points of local consonance at such ratios: these ratios occur precisely at steps of the scale. Such timbres tend to minimize the cost C.
This insight can be exploited in two ways. First, it can be used to reduce the search space of the optimization routine. Instead of searching over all frequencies in a bounded region, the search need only be done over induced timbres. More straightforwardly, the timbre selection problem for equal tempered scales can be solved by careful choice of induced timbres.
As an example, consider the problem of designing timbres to be played in 10 tone equal temperament. 10-tone is often considered one of the worst temperaments for harmonic music, since the steps of the ten tone scale are distinct from the (small) integer ratios, implying that harmonic timbres are very dissonant. The principle of local consonance asserts that these intervals will become more consonant if played with correctly designed timbres. Here are three timbres induced by the 10 tone equal tempered scale. Let b = the 10th root of 2.
(f, b10 f , b17 f , b20 f , b25 f , b28 f , b30 f )
(f, b7 f , b16 f , b21 f , b24 f , b28 f , b37 f )
(f, b7 f , b13 f , b17 f , b23 f , b28 f , b30 f )
The dissonance curves of these timbres are
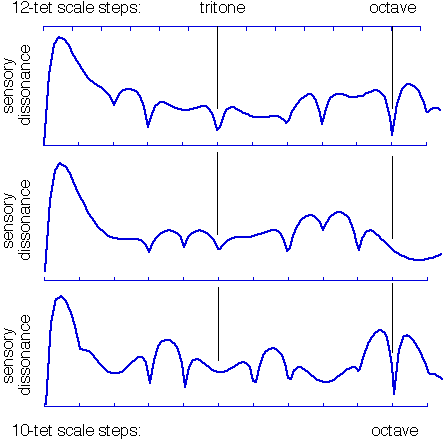
They really are consonant when played on a 10 tone equal tempered scale. Not surprisingly, the same tones sound quite dissonant when played in a standard 12 tone scale. Analogous arguments suggest that the consonance of 12- tone equal tempered tuning can be maximized by moving the partials away from the harmonic series to a series based on b = the twelfth root of 2.
Any arbitrary timbre (set of frequencies and amplitudes) can be realized with the aid of a computer. Is it always possible to design acoustic instruments that will have a given timbre? How about brasses? Fletcher and Rossing proclaim that "If the flaring part of the horn extends over a reasonable fraction of the total length, for example around one third, then there is still enough geometrical flexibility to allow the frequencies of all modes to be adjusted to essentially any value desired." With stringed instruments, the trick is to find a variable thickness string that will vibrate with partials at the desired frequencies. The partials of a drumhead can be tuned by weighting or layering sections of the drumhead. The partials of reed instruments can be manipulated by the contour of the bore as well as the shape and size of the tone holes. Bells can be tuned by changing the shape and thickness of the walls. Exactly how to engineer acoustic instruments with specified timbres is an interesting issue.
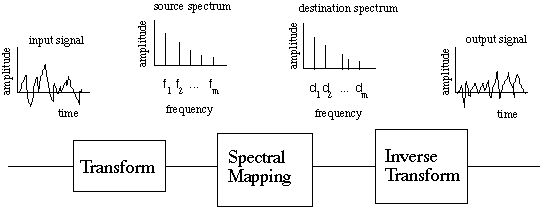
An easier approach is to synthesize the timbres. In the figure above, a harmonic waveform (which may be a sample of an acoustic instrument) is transformed into its constituent frequencies. The frequencies are changed in a systematic way that maps the partials into the specified timbre, and then transformed back into a useable waveform. The result is a nonharmonic timbre with much of the character of the original instrument. This is the key idea behind spectral mappings.
The principle of local consonance shows how to imagine a number of differently tuned orchestras, digital or acoustic, each with instruments designed with a particular timbre and played in the related tuning. How about a band of instruments tuned to stretched or compressed tunings? An orchestra optimized for seven or ten tone equal temperaments? A wind instrument with the timbre of a drum? A trumpet with the harmonic structure of a steel beam? The consonance curve shows how to properly tune the instrument. Using a computer to generate the timbres gives the ability to audition the design before building, saving time in the design and specification of nontraditional instruments.
The principle of local consonance shows how to relate timbres and tunings. Two complementary computational techniques were proposed: a way to find consonant scales given a specified timbre, and a way to find consonant timbres given a specified scale. One implication is that the musical notion of consonance of intervals such as the octave and fifth can be viewed as a result of the timbre of the instruments we typically use. The justly intoned scales can similarly be viewed as a consequence of the harmonic timbres of musical instruments.
The advent of inexpensive musical synthesizers capable of realizing arbitrary sounds allows exploration of nonharmonic acoustic spaces. The principle of local consonance provides guidelines on how to sensibly relate tuning and timbre. More ambitiously, it is easy to imagine new nonharmonic instruments capable of playing consonant music. The computational techniques of this paper allow specification of timbres and tunings for such instruments.
For Further Reading...
W. Carlos, "Tuning: At the Crossroads," Computer Music Journal, Spring, 29-43 (1987).
J. M. Chowning, "The Synthesis of Complex Audio Spectra by Means of Frequency Modulation," J. Audio Engineering Society, Vol. 21, 526-534 (1973).
N. H. Fletcher and T. D. Rossing, The Physics of Musical Instruments, Springer-Verlag (1991).
S. Goldberg, Genetic Algorithms in Search, Optimization, and Machine Learning, Addison-Wesley, New York, NY (1989)
H. Helmholtz, On the Sensations of Tones, Dover, New York (1954).
S. Kirkpatrick, C. D. Gelatt, M. P. Vecchi, "Optimization by Simulated Annealing," Science, vol. 220, No., 4598, May (1983).
M. V. Mathews and J. R. Pierce, "Harmony and Nonharmonic Partials," Journal of the Acoustical Society of America 68, 1252-1257 (1980).
M. V. Mathews, J. R. Pierce, A. Reeves, and L. A. Roberts, "Theoretical and Experimental Explorations of the Bohlen-Pierce Scale," Journal of the Acoustical Society of America. 84, 1214-1222 (1988).
J. R. Pierce, "Attaining Consonance in Arbitrary Scales,"Journal of the Acoustical Society of America. 40, 249 (1966).
R. Plomp and W. J. M. Levelt, "Tonal Consonance and Critical Bandwidth," Journal of the Acoustical Society of America.38, 548-560 (1965).
W. A. Sethares, "Local Consonance and the Relationship Between Timbre and Scale"
F. H. Slaymaker, "Chords from Tones Having Stretched Partials," Journal of the Acoustical Society of America. 47, 1469-1571 (1968).
S. R. Wilkinson, Tuning In, Hal Leonard Books, (1988).
For Further Listening...
![]()
To get to back to my homepage, click here, and dont forget to check out my book Tuning Timbre Spectrum Scale