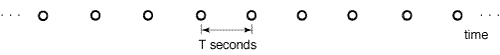|
|
Rhythm, Periodicity, Regularity, Recurrence |
Mathematics helps explain the patterns and rhythms of the universe. Music helps us synchronize to those patterns. (paraphrased from Math and Music: Harmonious Connections)
|
|
Rhythm, Periodicity, Regularity, Recurrence |
Mathematics helps explain the patterns and rhythms of the universe. Music helps us synchronize to those patterns. (paraphrased from Math and Music: Harmonious Connections)
|
recurs at predictable intervals, in this case, every six elements. Thus one component of periodicity is the rate of recurrence, called the period. But what is it that is repeating? Is it the six element pattern
c 3 # À m ©
or is it this pattern
# À m © c 3
Evidently, the two descriptions are on equal logical footing since they are identical except for the starting element.
While any of the possible six element patterns may be equal on a
logical footing, they may not be equal on a perceptual footing. Look
again at the complete sequence.
For many observers, the ©
stands out from the others, creating a visually compelling reason to
place the © symbol at the start of the sequence. Thus,
perceptually, the sequence is perhaps best described by a repetition of
the pattern
|
though some might wish to place the © at the end. Thus the starting ambiguity may be resolved by choosing the position of one prominent element. This defines the phase of the sequence (by analogy with the phase of a sinusoid).
Analogous effects occur in the auditory realm. The rhythmic pattern shown in Fig. 3 is presented in the sound examples. In the first case, all notes are struck identically. Which note appears to start the pattern? The succeeding examples with N=1 to N=7 each single out one note (the notes are labeled N in the figure) to emphasize. In many cases (but not all) this changes the apparent starting note of the pattern.

An important feature of periodic phenomena is that they readily support hierarchical structures. For example, by emphasizing every other c (making it large and bold), the visual focus changes from the © to the bold c.
|
Pairs of the six-term sequences become perceptually linked, creating a simple two-level hierarchy where each repetition (of twelve elements) consists of a pair of lower-level six-element terms. This is a visual analogy of metrical structure, as discussed in Chapter. 3.
Exact repetition and perfect periodicity are absent in an imperfect world. For example, in the visual pattern ...© c 3 # À m... there may be occasional mistakes. Maybe one out of every hundred symbols is randomly changed. Clearly, the sequence is still "mostly" periodic, and this kind of corruption is often described by saying that the periodic sequence has been contaminated with noise. (Observe that this use of noise is quite different from the use of noise in the sense of an annoying or undesirable sound, as in a hiss-filled recording or a noisy environment.) Another kind of deviation from periodicity occurs when the number of elements changes; perhaps one out of every hundred symbols is randomly deleted, or extra ones may be added.
In the auditory realm, this corresponds to a kind of jitter in the exact timing of events and of the underlying period. For example, in the final sound example in the sound series (N=8), the notes are all struck identically, but each note is displaced in time by a small random amount. Such small timing deviations may change the rhythm that is perceived.
Yet another kind of change in a periodic structure occurs when the period changes. Perhaps the six-element sequence is augmented to include a seventh element, increasing the underlying period to seven. Analogous changes are quite common in the auditory realm where they may be perceived as changes in tempo: faster tempos occur when there is a decrease in the period, slower tempos correspond to an increase in the underlying period. Alternatively, changes in period may be perceived as changes in pitch: lower pitches correspond to longer periods and higher pitches correspond to shorter periods.
Deviations from periodicity may occur in several ways:
- period
- phase or starting point
- the elements that are ordered within a single repetition
Moreover, periodic sequences may not be perceived straightforwardly: they may be perceived in different ways depending on the rate of presentation and they may be interpreted in hierarchical terms. Deviations from periodicity may influence (and be influenced by) the percieved hierarchies. As will become clear in later chapters, these basic notions of periodic sequences underlie many of the analytical tools that can be used to locate rhythmic phenomena. Deviations from periodicity will cause the bulk of the difficulties with these methods.
- elements may (occasionally) change
- elements may jitter in time (or the number of elements in a period may temporarily increase or decrease)
- the period may increase or decrease
The constant interaction between the physically measureable properties of a sequence and the human perception of those properties is fascinating. Think of a periodic sequence of identical clicks separated by a constant time interval, as is shown schematically in Fig. 4. Now listen to the Regular Interval 750 sound example. In the soundfile, the time interval between successive clicks is exactly 750 ms. Does it sound perfectly regular? Almost invariably, listeners begin "counting" the clicks. The inner ear may count 1-2-1-2 or perhaps 1-2-3-1-2-3. Many people report hearing 1-2-3-4-1-2-3-4. Almost no one hears this as it truly is: a repetition of exactly identical clicks. Consider the implication; the ear creates an ordered pattern (the apparent repetition of the clicks in units of 2, 3, or 4) where none objectively exists.