What is a periodicity transform?

It is a way to automatically detect periodicities.

To give you an idea of what the Periodicity Transform is good at, let's look at a simple example. Here is a data record that I constructed by adding together two periodic sequences, one with period 13 and the other with period 19. For good measure, I added about 25% noise. The result looks like this:

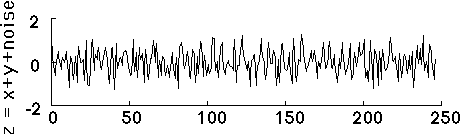
It's not so easy to "see" the two periodic sequences that are buried inside, is it? If we take the Fourier transform (DFT), then we get:

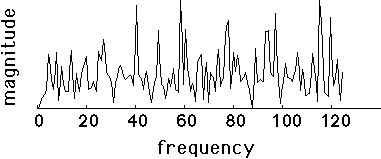
Again, its pretty difficult to see any pattern here. The 13-periodic and the 19-periodic sequences are still hidden. Now let's apply the periodicity transform called the "M-Best" algorithm, which searches for the M largest periodicities. With M=10, we get:

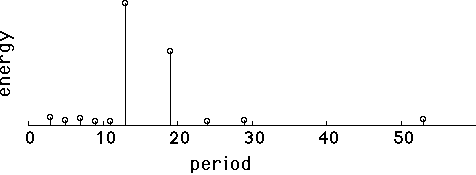
Now that's more like it! The two periods (at 13 and 19) are clearly visible. The other eight small periods reflect minor accidental patterns that happen to occur in the noise. The Periodicity Transforms are good at finding periodicities in data.

Most standard transforms can be interpreted as projections onto suitable subspaces, and in most cases (such as the Fourier and Wavelet transforms), the subspaces are orthogonal. Such orthogonality implies that the projection onto one subspace is independent of the projection onto others. Thus a projection onto one sinusoidal basis function (in the Fourier Transform) is independent of the projections onto others, and the Fourier decomposition can proceed by projecting onto one subspace, subtracting out the projection, and repeating. Orthogonality guarantees that the order of projection is irrelevant. This is not true for projection onto nonorthogonal subspaces such as the periodic subspaces Sp. Thus the order in which the projections occur effects the decomposition, and the Periodicity Transform does not in general provide a unique representation. Once the succession of the projections is specified, however, then the answer is unique.

The Periodicity Transform searches for the best periodic characterization of the length N signal x. The underlying technique is to project x onto some periodic subspace Sp. This periodicity is then removed from x leaving the residual r stripped of its p-periodicities. Both the projection x and the residual r may contain other periodicities, and so may be decomposed into other q-periodic components by further projection onto Sq. The trick in designing a useful algorithm is to provide a sensible criterion for choosing the order in which the successive p's and q's are chosen. The intended goal of the decomposition, the amount of computational resources available, and the measure of "goodness-of-fit" all influence the algorithm. Our paper discusses four ways to mind our p's and q's.

(1) The "small to large" algorithm assumes a threshold T and calculates the projections onto Sp beginning with p=1 and progressing through p=N/2. Whenever the projection contains at least T percent of the energy in x, then the corresponding projection is chosen as a basis element.

(2) The "M-best" algorithm maintains a list of the M best periodicities and the corresponding basis elements. When a new (sub)periodicity is detected that removes more power from the signal than one currently on the list, the new one replaces the old, and the algorithm iterates.

(3) The "best-correlation" algorithm projects x onto all the periodic basis elements, essentially measuring the correlation between x and the individual periodic basis elements. The p with the largest (in absolute value) correlation is then used for the projection.

(4) The "best-frequency" algorithm determines p by Fourier methods and then projects onto Sp.