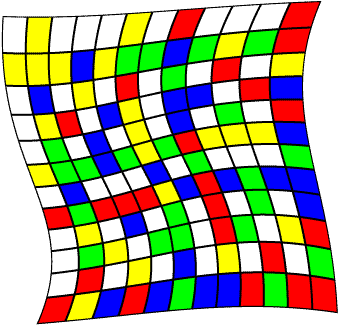
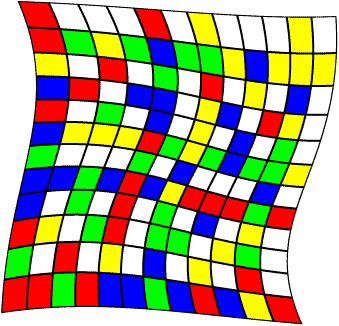
Variations of the Fibonacci Checkerboard

Fibonacci Checkers (or more simply, Slide Checkers) is a strategy game for two, three, or four players. It is played on a colorful board

that is generated from the well known Fibonacci numbers. To see how the game is played, here are the complete rules and here is a description of where the playing board comes from.

In the original sequence investigated by Count Fibonacci

1, 1, 2, 3, 5, 8, 13, 21, 34, ...

each number is equal to the sum of the two previous numbers. Thus the next term of the sequence will be 21+34=55. In symbols, the new number in the i+1st place is equal to the number in the ith slot plus the number in the i-1st place, which can be written:

x(i+1) = x(i) + x(i-1).

There are many possible variations on this idea. For instance, successive numbers could be chosen to be the weighted sum of the two previous numbers. In symbols:

x(i+1) = a x(i) + b x(i-1)

where a and b are two integers. For example, if a=2 and b=1, the sequence would be

1, 1, 3, 7, 17, 41, ...

If these numbers are taken modulo 12, and each possible starting sequence is colored uniquely, then new 12x12 playing boards result. Here are some of my favorites. With a=5 and b=1:

With a=7 and b=1:

With a=11 and b=1:

With a=1 and b=7:

And finally, with a=5 and b=7:

Of course, there is nothing sacred about these particular numbers, but they seem to me to give the best playing surfaces for Fibonacci or Slide checkers. If you know Matlab, you can generate your own boards (of any size) using the Matlab code. Here is a photo of a slide checkerboard that my dad made several years ago. In the photo you may notice that he is just about to make a bad move. There are also several possible variations on the playing surface. The rules to the game are simple, good strategies may not be so easy. Good luck and have fun!

To get to my homepage, click here.